組合せゲーム理論を用いたゲームの解析
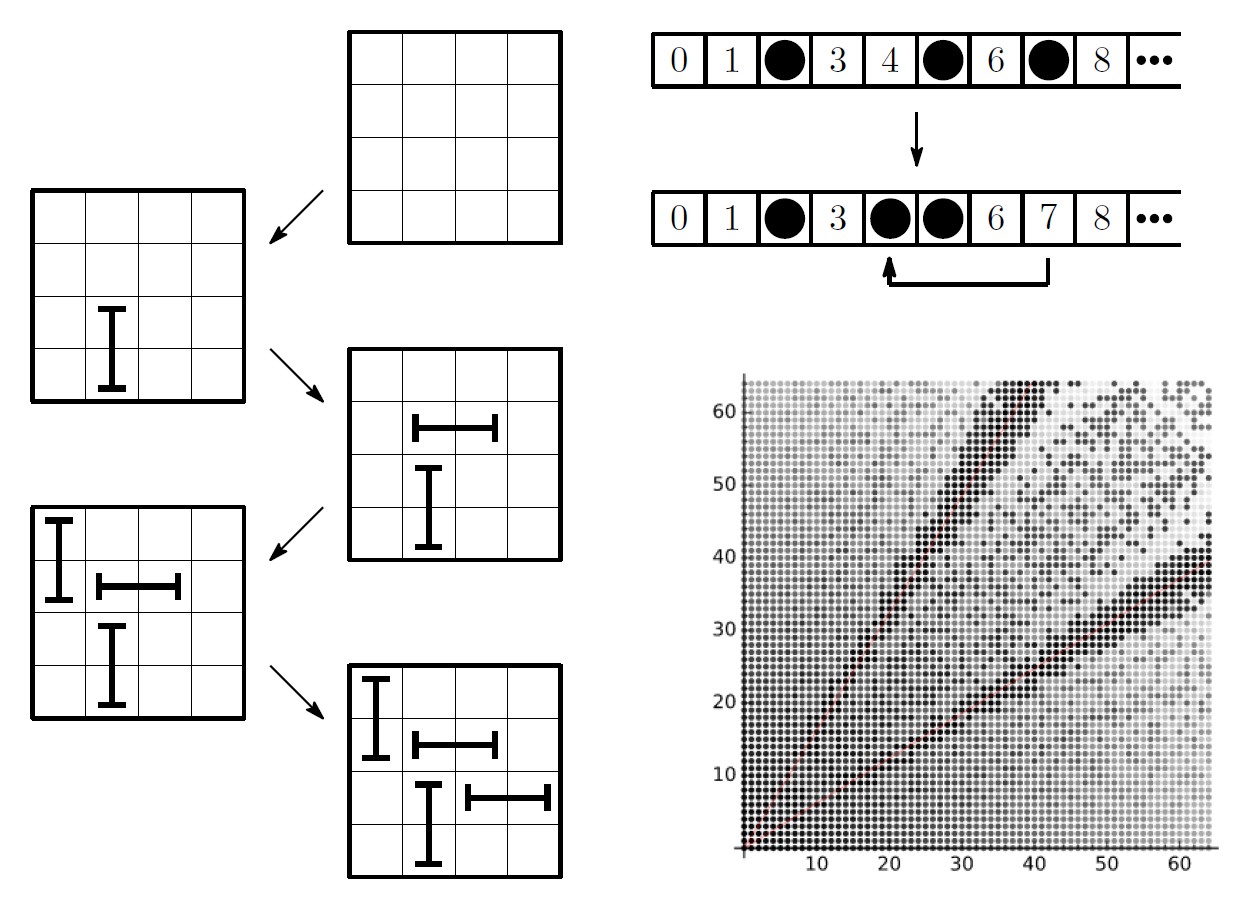
組合せゲーム理論は2人のプレイヤーが交互に「手」をプレイして勝敗を決めるタイプのゲームを数学的に解析する理論として、近年急速に発展している分野です。様々なゲームに対して理論を適用し、ルールの違いが勝敗にどのような影響を及ぼすかを研究します。
講座・教員 齋藤夏雄 教授 Saito Natsuo
研究テーマ
代数学およびその情報科学分野への応用
群論を用いたパズルの数学的構造の研究
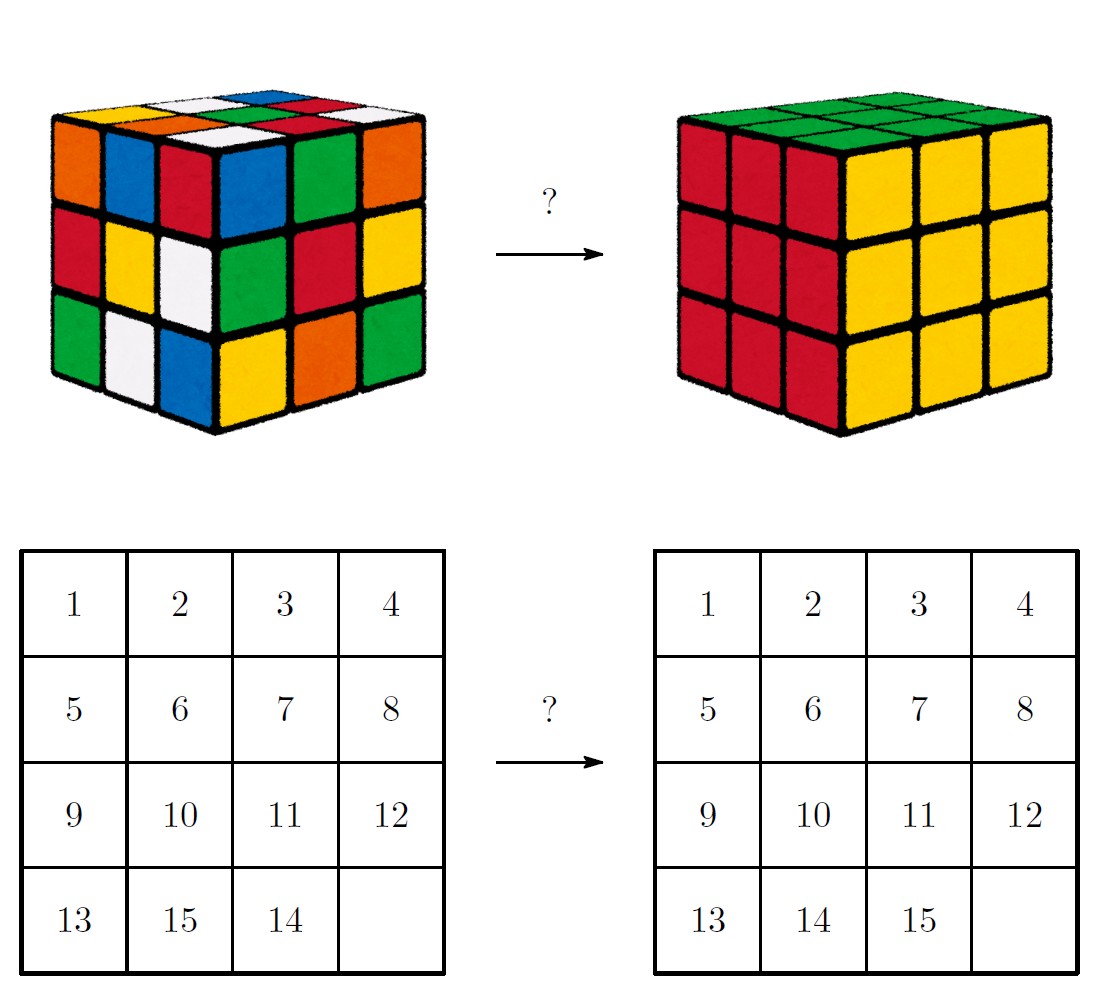
代数学に群論と呼ばれる分野があります。これをうまく使うと、ルービックキューブやスライディングブロックパズルなど、いくつかのピースを移動させたり組み替えたりするパズルの数学的な構造を調べることができます。
代数幾何学とその符号理論・暗号理論への応用
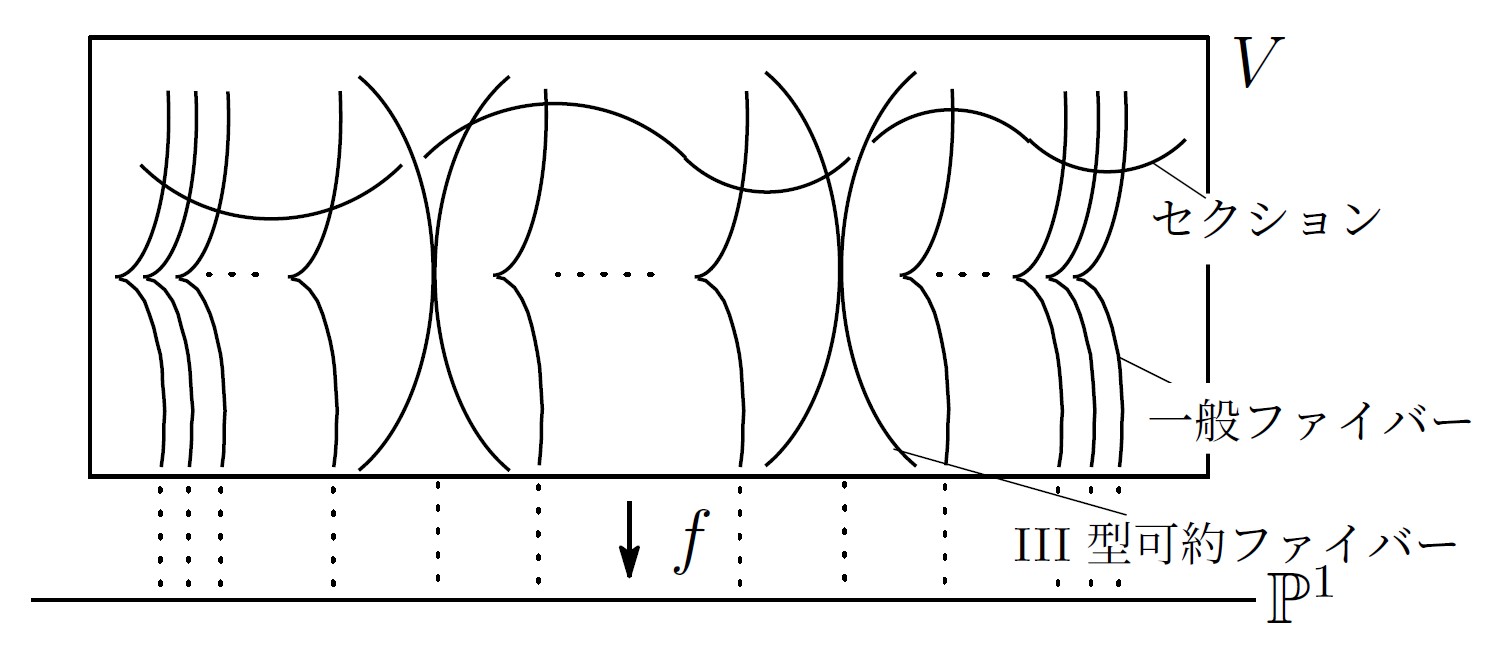
代数幾何学は主に代数学と幾何学にまたがる分野で、曲線や曲面などの「代数多様体」と呼ばれる数学的対象を、代数を用いて研究する分野です。1次元、2次元の代数多様体である代数曲線、代数曲面の構造を調べ、それを利用して線形符号や暗号を構成する研究を行います。